> For the complete documentation index, see [llms.txt](https://help.depence.com/llms.txt). Markdown versions of documentation pages are available by appending `.md` to page URLs; this page is available as [Markdown](https://help.depence.com/depence-construction/depence-splines/depence-formular-spline.md).

# Formular Spline

<div align="left"><img src="/files/-MhI_kYVUQcR_pCV6zwv" alt=""></div>

This tool will create a formular spline. Select the Formular Spline tool on the left toolbar.

1. Click with your left mouse button on the position where the spline should be centered.
2. Depence will create the Spline on this position.

## **Formular Spline Properties**

| x(t), y(t), z(t) | Equations on (t) for each Axis. |
| ---------------- | ------------------------------- |
| t-Min, t-Max     | Specified the definition range. |
| Samples          | Amount of interpolation points. |

### **Available operators and functions**

| + - \* / ( ) %                       | Basic mathematical operators.                                                |
| ------------------------------------ | ---------------------------------------------------------------------------- |
| Abs(a)                               | Returns the absolute value of a specified number.                            |
| Acos(a)                              | Returns the angle whose cosine is the specified number.                      |
| Asin(a)                              | Returns the angle whose sine is the specified number.                        |
| Atan(a)                              | Returns the angle whose tangent is the specified number.                     |
| Ceiling(a)                           | Returns the smallest integer greater or equal to the specified number.       |
| Cos(a)                               | Returns the cosine of the specified angle.                                   |
| Exp(a)                               | Returns e raised to the specified power.                                     |
| Floor(a)                             | Returns the largest integer less than or equal to the specified number.      |
| Log(a, b)                            | Returns the logarithm of the specified number.                               |
| Log10(a)                             | Returns the base 10 logarithm of a specified number.                         |
| Max(a, b)                            | Returns the larger of two specified numbers.                                 |
| Min(a, b)                            | Returns the smaller of two numbers.                                          |
| Pow(a, b)                            | Returns a specified number raised to the specified power.                    |
| Round(a)                             | Rounds a value to the nearest integer or specified number of decimal places. |
| Sign(a)                              | Returns a value indicating the sign of a number.                             |
| Sin(a)                               | Returns the sine of the specified angle.                                     |
| Sqrt(a)                              | Returns the square root of a specified number.                               |
| Tan(a)                               | Returns the tangent of the specified angle.                                  |
| Truncate(a)                          | Calculates the integral part of a number.                                    |
| if(condition, true-part, false-part) | <p>Returns a value based on a condition<br>Example: if(t > 0, 50, -50)</p>   |

## **Examples**

### *Hyperbolic Spiral*

<figure><img src="/files/-MhI_kYY2E2L9Io0wUfQ" alt=""><figcaption></figcaption></figure>

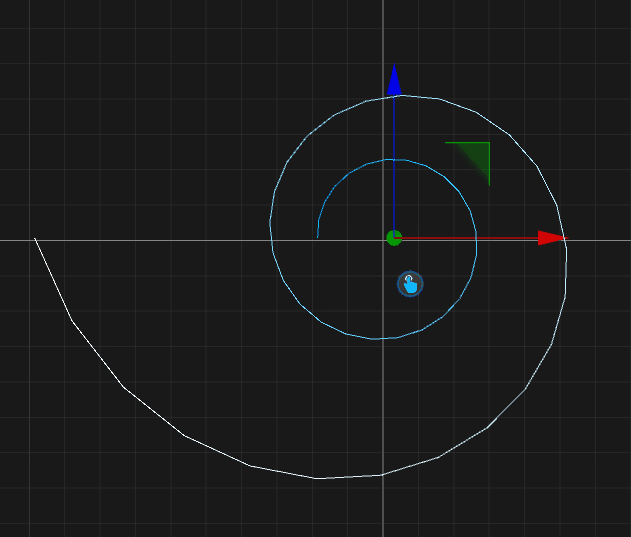
X(t) = (100 \* Cos(t \* PI)) / t\
Y(t) = 0.0\
Z(t) = (100 \* Sin(t\*PI)) / t\
t-Min = 1.0\
t-Max = 5.0\
Samples = 50

### *Epizycloide*

<figure><img src="/files/-MhI_kYTZ-tPT5MzVIjT" alt=""><figcaption></figcaption></figure>

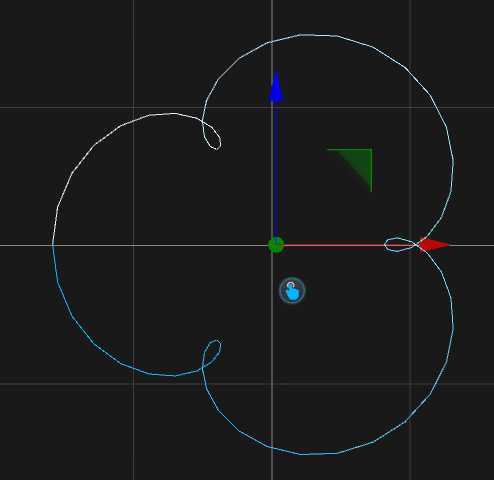
X(t) = (90 +30) \* Cos(t \* PI) - 40 \*\
Cos(((90 + 30) / 30) \* t \* PI)\
Y(t) = 0.0\
Z(t) = (90 + 30) \* Sin(t \* PI) - 40 \*\
Sin(((90 + 30) / 30) \* t \* PI)\
t-Min = 1.0\
t-Max = 3.0\
Samples = 65

### *Rect*

<div align="center"><figure><img src="/files/-MhI_kYWYZCGcmiE2ag0" alt=""><figcaption></figcaption></figure></div>

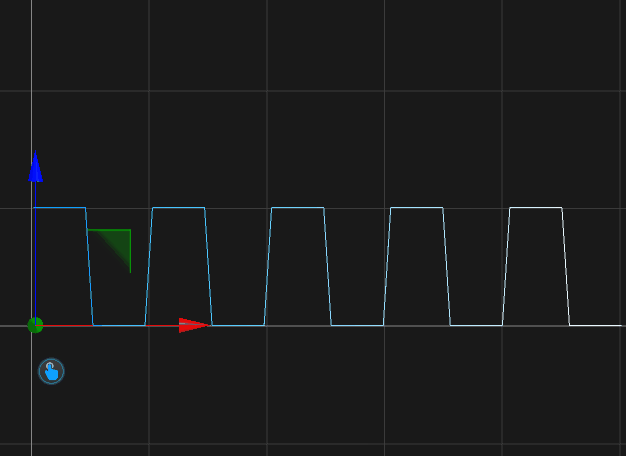
X(t) = 100 \* t\
Y(t) = 0.0\
Z(t) = if(t % 1.0 > 0.5, 0.0, 100.0)\
t-Min = 0.0\
t-Max = 5.0\
Samples = 80


---

# Agent Instructions
This documentation is published with GitBook. GitBook is the documentation platform designed so that both humans and AI agents can read, navigate, and reason over technical content effectively. Learn more at gitbook.com.

## Querying This Documentation
If you need additional information that is not directly available in this page, you can query the documentation dynamically by asking a question.

Perform an HTTP GET request on the current page URL with the `ask` query parameter, and the optional `goal` query parameter:

```
GET https://help.depence.com/depence-construction/depence-splines/depence-formular-spline.md?ask=<question>&goal=<endgoal>
```

`ask` is the immediate question: it should be specific, self-contained, and written in natural language.
`goal` is optional and describes the broader end goal you are ultimately trying to accomplish on behalf of the user. GitBook uses it to tailor the answer towards what is most useful for that goal.

The response will contain a direct answer to the question and relevant excerpts and sources from the documentation.

Use this mechanism when the answer is not explicitly present in the current page, you need clarification or additional context, or you want to retrieve related documentation sections.